RegressRangers

Welcome to our proposal website. Our chosen theme is Geographically Weighted Regression Models.
Author
Affiliation
Team 11

Singapore Management University

Published

March 3, 2023

Modified

April 16, 2023

Problem Statement

Many real-world phenomena exhibit significant spatial variability, and traditional regression models that assume spatial homogeneity fail to capture the underlying patterns in the data set collected. Geographically weighted regression models are an effective way to address this problem by allowing for local variation in the relationship between the response variable and the predictor variables. However, creating accurate geographically weighted regression models can be a complex and time-consuming process that requires specialized knowledge and software. Additionally, evaluating the performance of these models can be challenging due to the local nature of the models.

Case Study

Analysing vaccination rates is crucial in the current climate as the world is grappling with a global pandemic caused by COVID-19. Vaccination ๐Ÿ’‰ is one of the most effective ways to prevent the spread of infectious diseases and protect communities from illness and death. With the availability of COVID-19 vaccination data, we can gain important insights into the progress of immunization campaigns and help identify areas where more resources and efforts are needed to increase vaccine uptake. Additionally, analyzing vaccination rates can inform public health policies and interventions aimed at improving vaccine distribution, accessibility, and equity, particularly for vulnerable populations who may face barriers to vaccination.

We will be using the above-mentioned case study to design and test our geospatial analytics tool ๐Ÿ˜ƒ

Key Objectives

Our project aims to create a web-based geospatial analytics tool that helps users create and evaluate geographical regression models easily by:

  • importing data ๐Ÿ“

  • identifying significant regressors in the model ๐Ÿ”

  • creating customised Linear and Geographically Weighted Models ๐Ÿ“ˆ

  • understanding the models based on a variety of statistical results๐Ÿงช

To build and test our application, we will be modeling the vaccination rate of DKI, Jakarta in the various sub-districts based on a variety of socio-economic factors.

Table 1: Datasets used
Name Source
2019 DKI Jakarta Census data DKI Jakarta Census Data
COVID-19 cases data in DKI Jakarta District based COVID-19 data
Vaccination Rate data in DKI Jakarta District based Vaccination data

We have identified studies that have attempted to perform similar types of analyses:

1. Spatial Modeling of COVID-19 Vaccine Hesitancy in the United States
Table 2: Details of Study #1
Objective This study examines the spatial distribution of vaccination rates in the United States and identifies significant covariates using multiscale geographically weighted regression, which can be used as a reference for region-specific policies in monitoring vaccination programs.
Methodology

  • OLS regression model.

  • GWR model using adaptive kernel.

  • MGWR model using bi-square kernel for weighting data and AICc (i.e., Akaike Information Criteria) to determine optimal bandwidths.
Key Learning Points

  • Provide multiple models to provide most accurate results through comparison and validation.

  • Use stepwise forward regression, Adj.\(R^2\), \(VIF\), and \(r\) to exclude insignificant variables.

  • Use adaptive bandwidth to weight the data within the bandwidth and use AICc to find optimal bandwidths.
Areas for Improvement
  • The GWR model disregards the possibility that the covariates affecting the vaccination rate are often at different scales (bias the result by exaggerating or underestimating).
2. Application of geographically-weighted regression analysis to assess risk factors for malaria hotspots in Keur Soce health and demographic surveillance site
Table 3: Details of Study #2
Objective This study investigated malaria hotspots in Keur Soce sites by using geographically-weighted regression. Because of the occurrence of hotspots, spatial modelling of malaria cases could have a considerable effect in disease surveillance.
Methodology

  • OLS

  • GWR - Linear Regression used as a diagnostic tool for selecting predictors for this model.

  • Assessment of model:

    • Multicollinearity was assessed with \(VIF\).

    • Autocorrelation statistic was applied to detect whether there is spatial autocorrelation or clustering of residuals.

    • Spatial Independency of residuals was assessed with Moranโ€™s I.
Key Learning Points

  • GWR coefficient values can be used to explore the spatial variability of relationships between malaria incidence or persistence and selected factors.

  • We should use AICc to determine the optimal bandwidth of the kernel function.
Areas for Improvement
  • NIL
3. A geographically weighted regression approach to investigate the effect of traffic conditions and road characteristics on air pollutant emissions
Table 4: Details of Study #3
Objective
  • This study aims to investigate the effects of traffic, road network, employment and social demographic characteristics on air pollutant emissions at the level of traffic analysis zone (TAZ).
  • In deriving an appropriate regression model, the authors also compared the use of geographically weighted regressions and the conventional generalised linear regression model to link pollutant concentrations with various contributory variables.
Methodology

  • Linear Regression analysis - if a candidate variable and its quadratic and cubic terms are all insignificant, this variable will not be retained in the GWR models

  • Pearson Correlation Coefficients were calculated to ensure highly correlated variables were not simultaneously included in the model.

  • Best combination of explanatory variables determined by AICc.

  • GWR model - used Kriging Interpolation method to get the pollutant concentrations

    • correlation analysis conducted between candidate exploratory variables

  • Used 10-fold cross validation of different models to infer how much prediction accuracy increases based on changes made to the model
Key Learning Points

  • GWR can effectively overcome the limitation of Generalised Linear Model (GLM) in modeling the pollutant concentrations at the Traffic Analysis Zone (TAZ) level.

  • Constraining the parameters to be constant may lead to biased parameter estimates.
Areas for Improvement
  • NIL
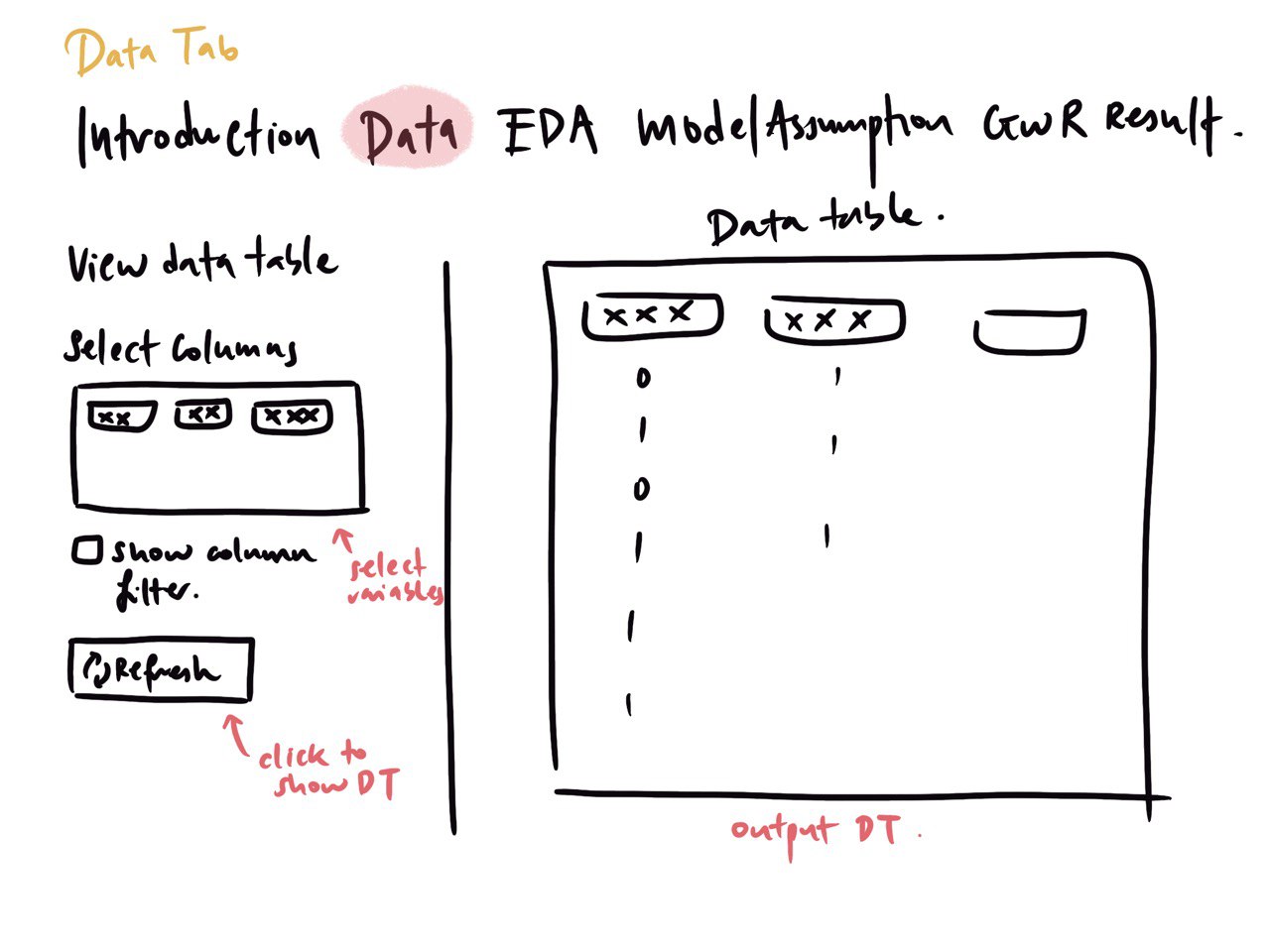
  1. Data Visualisation

    • Import data into R environment

    • Show data in tabular format

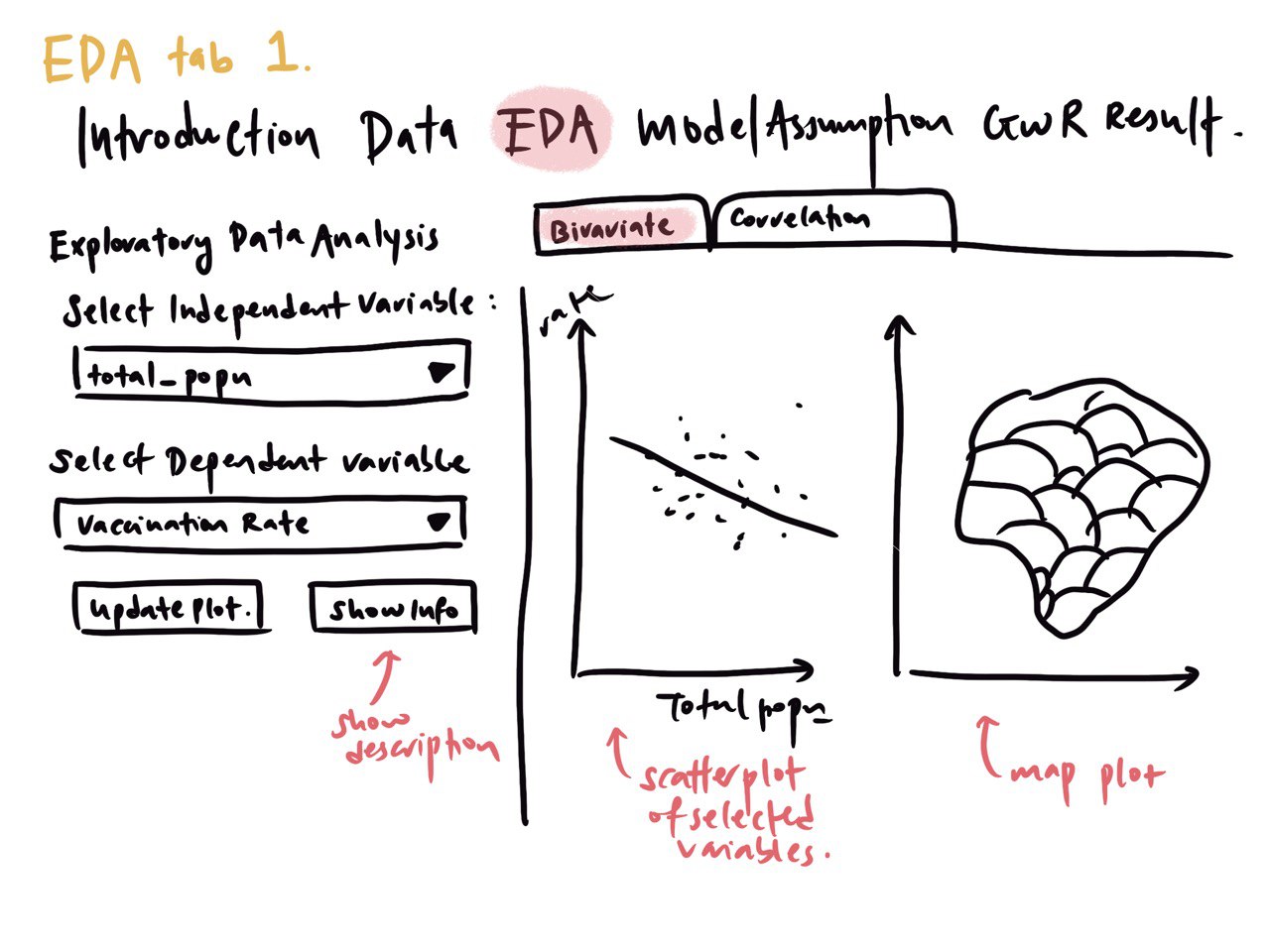
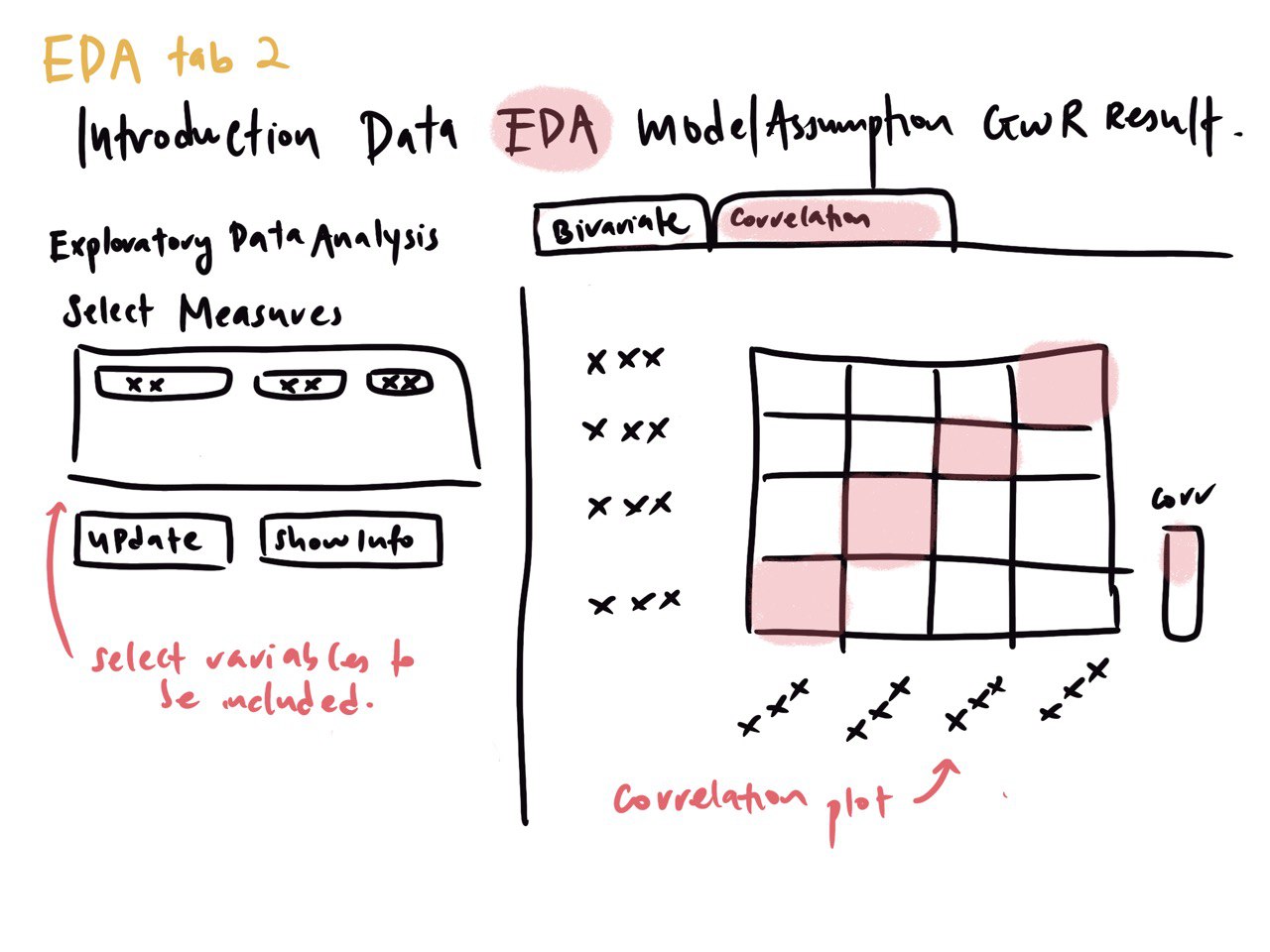
  2. Exploratory Data Analysis (EDA)
    EDA helps users to understand the data distribution, detect outliers, and identify any missing values. This helps us evaluate the that the assumptions of statistical tests are met before performing them. EDA also helps users generate hypotheses that can guide further investigations of the issue at hand.

    • Draw Histograms

    • Create Choropleth Map

    • Correlation Plot

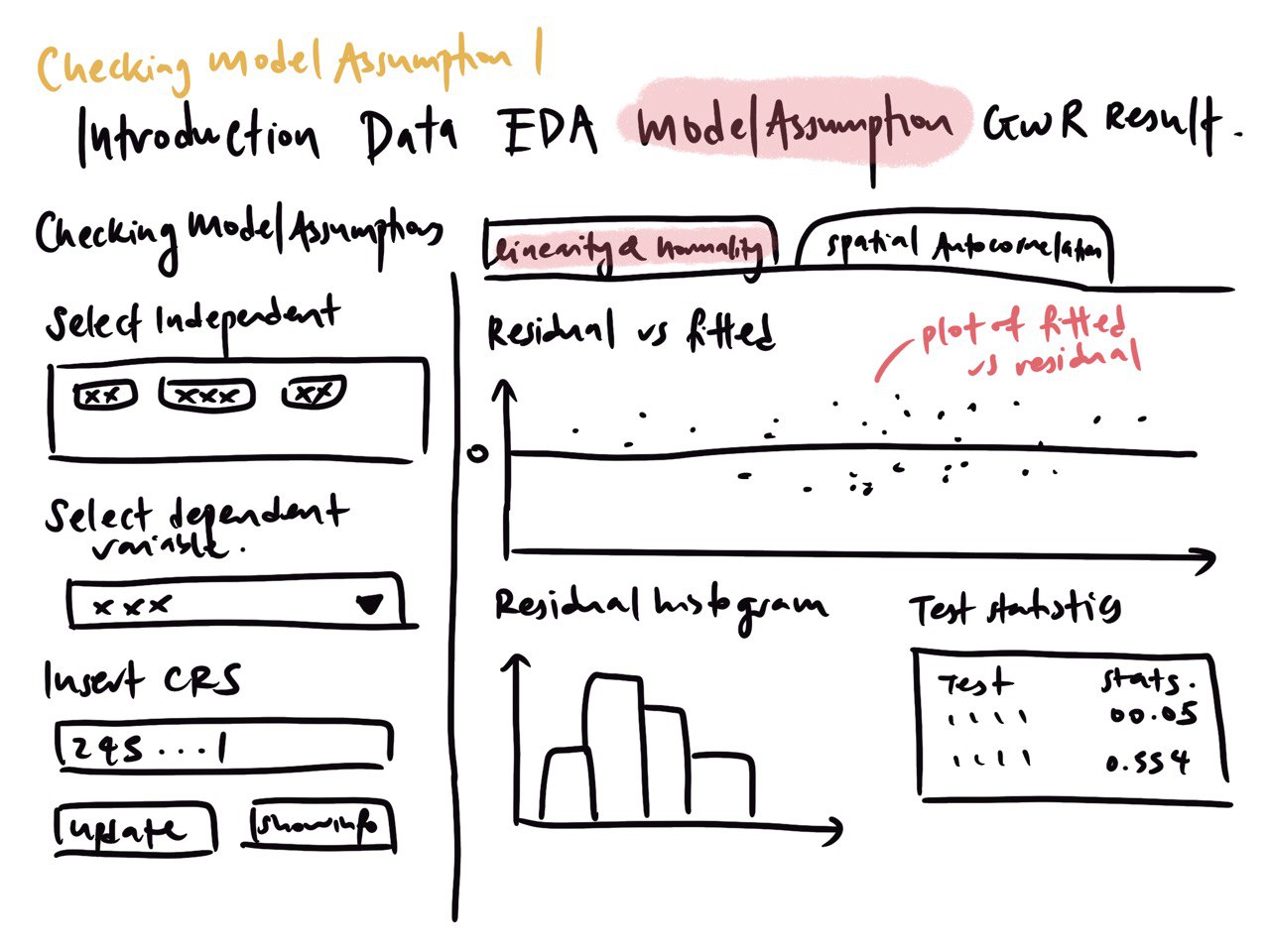
  3. Linear Regression (OLS)
    Performing Ordinary Least Squares regression before GWR is important as it provides a globel model for the data. It can help identify overall trends and relationships in the data. By comparing the results of OLS and GWR, users can better understand how relationship between variables vary across space and make more informed decisions.

    • Generalised Multiple Linear Regression Method

    • Residual Plot

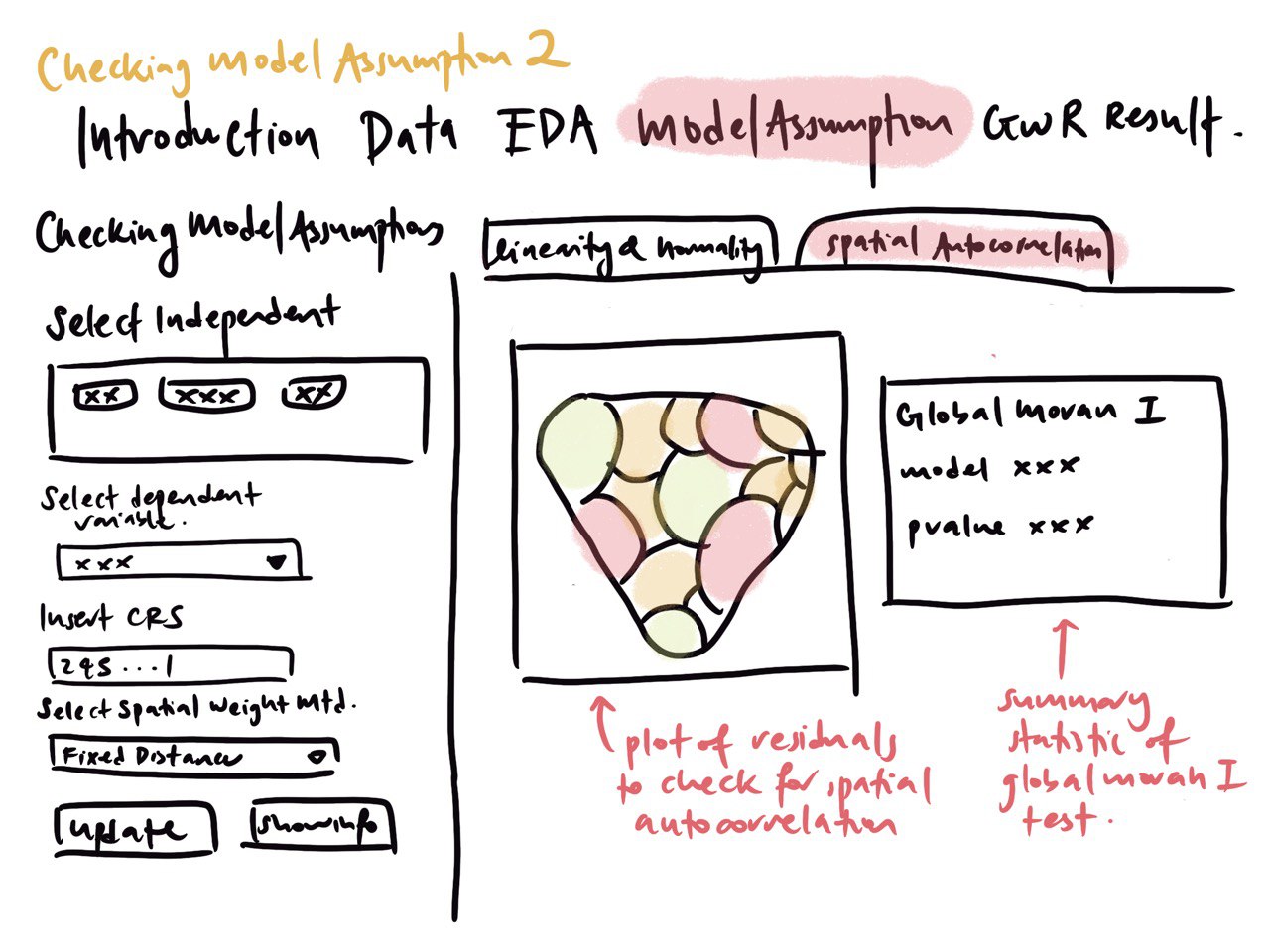
    • Check for spatial autocollinearity

    • Check linearity and normality assumptions

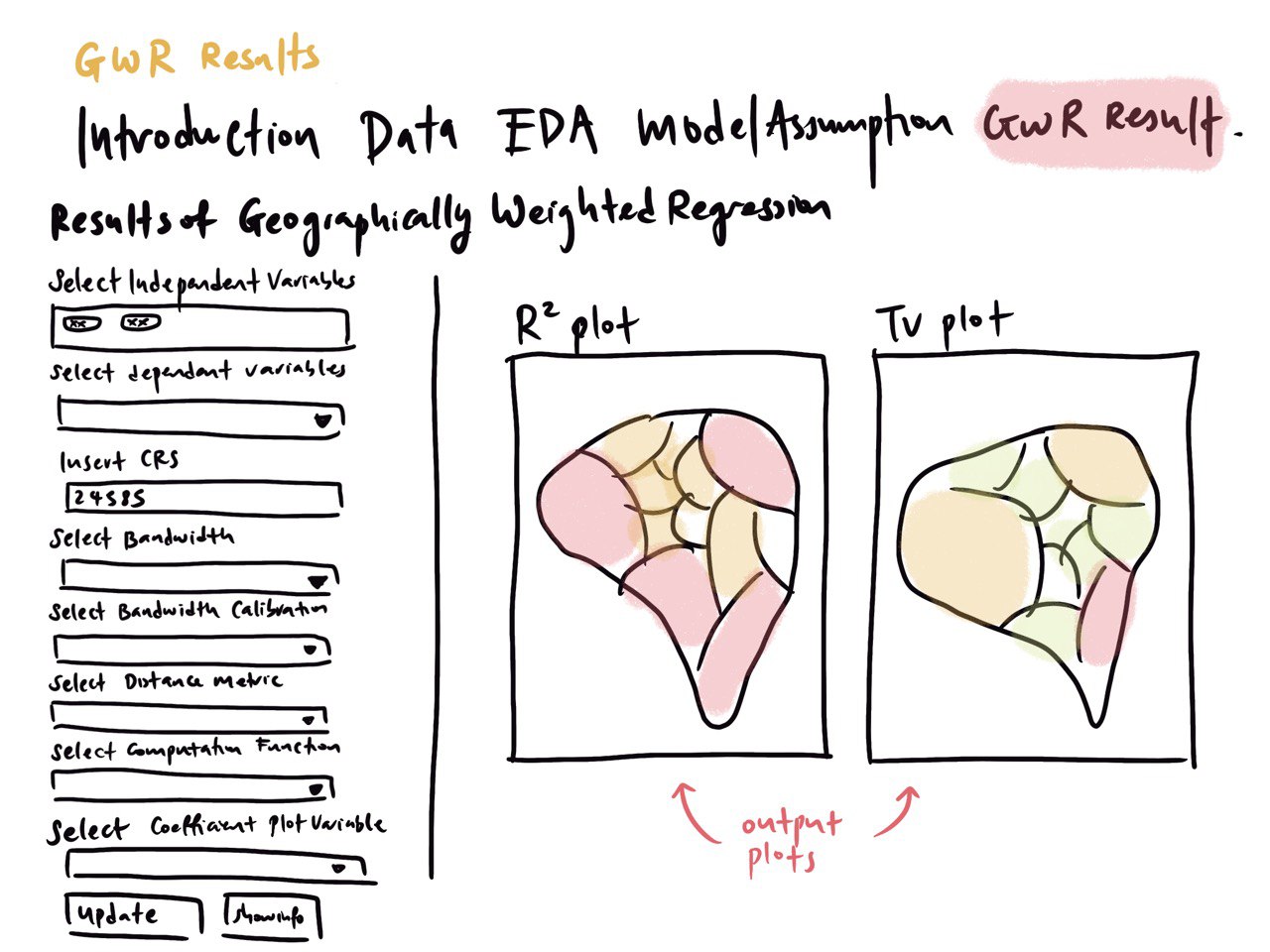
  4. Geographically Weighted Regression (GWR)
    As mentioned in our Problem Statement, GWR helps users determine significant covariates because it allows for the estimation of local regression coefficients that could vary spatially but not revealed in a global model (such as OLS)
    • R2 Plot
    • Coefficient t-value plot

This list is not exhaustive and we might add more libraries as we design and test the analytics tool.

  • sf - import geospatial data using approproate function(s)

  • readr - import csv files

  • dplyr - to perform relation joins

  • spdep - for computation of spatial weights and calculate spatially lagged variables

  • tmap - for plotting cartographic quality static point pattern maps or interactive maps using leaflet API

  • tidyverse - this is a collection of packages for performing data science tasks such as wrangling and visualising data

Credit to TeamGantt for their gantt chart template.

  • Mollalo, A., & Tatar, M. (2021). Spatial Modeling of COVID-19 Vaccine Hesitancy in the United States. International journal of environmental research and public health, 18(18), 9488. https://doi.org/10.3390/ijerph18189488

  • Ndiath, M. M., Cisse, B., Ndiaye, J. L., Gomis, J. F., Bathiery, O., Dia, A. T., Gaye, O., & Faye, B. (2015). Application of geographically-weighted regression analysis to assess risk factors for malaria hotspots in Keur Soce health and demographic surveillance site. Malaria journal, 14, 463. https://doi.org/10.1186/s12936-015-0976-9

  • Chengcheng, X., Jingya, Z., Liu, P. (2019). A geographically weighted regression approach to investigate the effects of traffic conditions and road characteristics on air pollutant emissions. Journal of Cleaner Production, Volume 239, 118084, ISSN 0959-6526, https://doi.org/10.1016/j.jclepro.2019.118084